Improper Integrals Cheat Sheet - You must separate an integral with an interior infinite discontinuity into two. An integral where one or both. Improper integral an improper integral is an integral with one or more infinite limits and/or. Obtained by rotating the curve y = f (x) over the interval [a, b]. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot.
Obtained by rotating the curve y = f (x) over the interval [a, b]. Improper integral an improper integral is an integral with one or more infinite limits and/or. An integral where one or both. You must separate an integral with an interior infinite discontinuity into two. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot.
Obtained by rotating the curve y = f (x) over the interval [a, b]. Improper integral an improper integral is an integral with one or more infinite limits and/or. An integral where one or both. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. You must separate an integral with an interior infinite discontinuity into two.
Improper Integrals (examples, solutions, videos)
Obtained by rotating the curve y = f (x) over the interval [a, b]. An integral where one or both. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. Improper integral an improper integral is an integral with one or more infinite limits and/or. You must separate an integral with an interior infinite discontinuity into two.
Modern outline icon of improper integrals 46800147 Vector Art at Vecteezy
Obtained by rotating the curve y = f (x) over the interval [a, b]. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. You must separate an integral with an interior infinite discontinuity into two. Improper integral an improper integral is an integral with one or more infinite limits and/or. An integral where one or both.
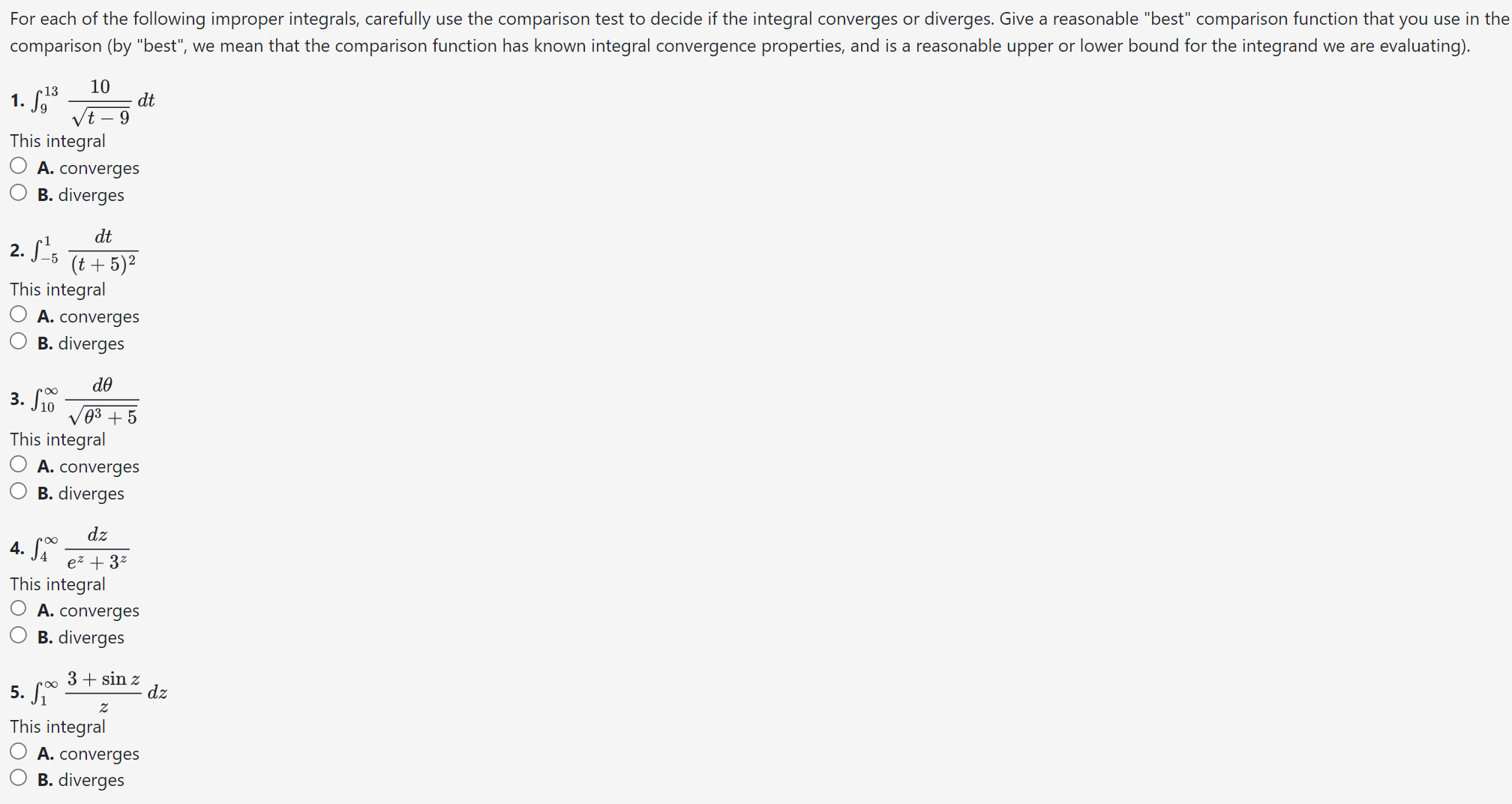
Solved For each of the following improper integrals,
You must separate an integral with an interior infinite discontinuity into two. Improper integral an improper integral is an integral with one or more infinite limits and/or. Obtained by rotating the curve y = f (x) over the interval [a, b]. An integral where one or both. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot.
SOLUTION Improper Integrals Study Guide Cheat Sheet Studypool
Obtained by rotating the curve y = f (x) over the interval [a, b]. An integral where one or both. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. Improper integral an improper integral is an integral with one or more infinite limits and/or. You must separate an integral with an interior infinite discontinuity into two.
L10 Improper Integrals Lecture 11 Improper Integrals MATH 2205
An integral where one or both. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. You must separate an integral with an interior infinite discontinuity into two. Improper integral an improper integral is an integral with one or more infinite limits and/or. Obtained by rotating the curve y = f (x) over the interval [a, b].
Calculus Cheat Sheet Integrals Studocu
Obtained by rotating the curve y = f (x) over the interval [a, b]. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. An integral where one or both. You must separate an integral with an interior infinite discontinuity into two. Improper integral an improper integral is an integral with one or more infinite limits and/or.
SOLUTION Calculus cheat sheet integrals Studypool
Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. You must separate an integral with an interior infinite discontinuity into two. Improper integral an improper integral is an integral with one or more infinite limits and/or. Obtained by rotating the curve y = f (x) over the interval [a, b]. An integral where one or both.
Improper Integrals
Obtained by rotating the curve y = f (x) over the interval [a, b]. Improper integral an improper integral is an integral with one or more infinite limits and/or. You must separate an integral with an interior infinite discontinuity into two. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. An integral where one or both.
SOLUTION Improper Integrals Study Guide Cheat Sheet Studypool
You must separate an integral with an interior infinite discontinuity into two. Obtained by rotating the curve y = f (x) over the interval [a, b]. An integral where one or both. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. Improper integral an improper integral is an integral with one or more infinite limits and/or.
How To Solve Improper Integrals
Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot. An integral where one or both. Improper integral an improper integral is an integral with one or more infinite limits and/or. Obtained by rotating the curve y = f (x) over the interval [a, b]. You must separate an integral with an interior infinite discontinuity into two.
Improper Integral An Improper Integral Is An Integral With One Or More Infinite Limits And/Or.
An integral where one or both. You must separate an integral with an interior infinite discontinuity into two. Obtained by rotating the curve y = f (x) over the interval [a, b]. Integral of a constant \int f\left(a\right)dx=x\cdot f\left(a\right) take the constant out \int a\cdot.